Answer:
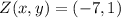
Explanation:
Given
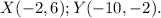
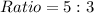
Required
Point Z
Given that the line segment XY is divided into ratio;
The coordinates of point Z can be calculated using ratio formula given below
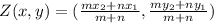
Where m and n are the ratio; m = 5 and n = 3
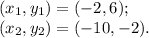
So,
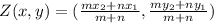 becomes
becomes

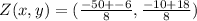
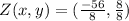
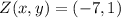
Hence, the coordinates of Z are (-7,1)