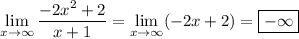Question

PRECAL:
Having trouble on this review, need some help.

Answer 1

1. As you can tell from the function definition and plot, there's a discontinuity at x = -2. But in the limit from either side of x = -2, f(x) is approaching the value at the empty circle:

`\displaystyle \lim_(x\to-2)f(x) = \lim_(x\to-2)(x-2) = -2-2 = \boxed{-4}`

Basically, since x is approaching -2, we are talking about values of x such x ≠ 2. Then we can compute the limit by taking the expression from the definition of f(x) using that x ≠ 2.

2. f(x) is continuous at x = -1, so the limit can be computed directly again:

`\displaystyle \lim_(x\to-1) f(x) = \lim_(x\to-1)(x-2) = -1-2=\boxed{-3}`

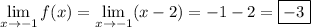
3. Using the same reasoning as in (1), the limit would be the value of f(x) at the empty circle in the graph. So

`\displaystyle \lim_(x\to-2)f(x) = \boxed{-1}`

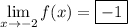
4. Your answer is correct; the limit doesn't exist because there is a jump discontinuity. f(x) approaches two different values depending on which direction x is approaching 2.

5. It's a bit difficult to see, but it looks like x is approaching 2 from above/from the right, in which case

`\displaystyle \lim_(x\to2^+)f(x) = \boxed{0}`

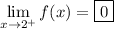
When x approaches 2 from above, we assume x > 2. And according to the plot, we have f(x) = 0 whenever x > 2.

6. It should be rather clear from the plot that

`\displaystyle \lim_(x\to0)f(x) = \lim_(x\to0)(\sin(x)+3) = \sin(0) + 3 = \boxed{3}`

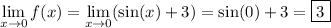
because sin(x) + 3 is continuous at x = 0. On the other hand, the limit at infinity doesn't exist because sin(x) oscillates between -1 and 1 forever, never landing on a single finite value.

For 7-8, divide through each term by the largest power of x in the expression:

7. Divide through by x². Every remaining rational term will converge to 0.

`\displaystyle \lim_(x\to\infty)(x^2+x-12)/(2x^2-5x-3) = \lim_(x\to\infty)\frac{1+\frac1x-(12)/(x^2)}{2-\frac5x-\frac3{x^2}}=\boxed{\frac12}`

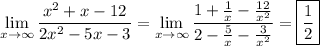
8. Divide through by x² again:

`\displaystyle \lim_(x\to-\infty)(x+3)/(x^2+x-12) = \lim_(x\to-\infty)\frac{\frac1x+\frac3{x^2}}{1+\frac1x-(12)/(x^2)} = \frac01 = \boxed{0}`

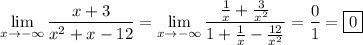
9. Factorize the numerator and denominator. Then bearing in mind that "x is approaching 6" means x ≠ 6, we can cancel a factor of x - 6:

`\displaystyle \lim_(x\to6)(2x^2-12x)/(x^2-4x-12)=\lim_(x\to6)(2x(x-6))/((x+2)(x-6)) = \lim_(x\to6)(2x)/(x+2) = (2*6)/(6+2)=\boxed{\frac32}`

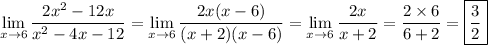
10. Factorize the numerator and simplify:

`(-2x^2+2)/(x+1) = -2 * (x^2-1)/(x+1) = -2 * ((x+1)(x-1))/(x+1) = -2(x-1) = -2x+2`

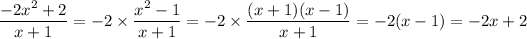
where the last equality holds because x is approaching +∞, so we can assume x ≠ -1. Then the limit is

`\displaystyle \lim_(x\to\infty) (-2x^2+2)/(x+1) = \lim_(x\to\infty) (-2x+2) = \boxed{-\infty}`