Question

Find the values of a , b , c in the equation
(X^5yz^4)^3\x^3yz=x^ay^bz^c

Answer 1

(a, b, c) = (12, 2, 11)

Explanation:

We assume you want to simplify ...

`((x^5yz^4)^3)/(x^3yz)=x^(3\cdot 5-3)y^(3\cdot 1-1)z^(3\cdot 4-1)=x^(12)y^2z^(11)`

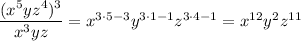
Compared to (x^a)(y^b)(z^c), we find that ...

(a, b, c) = (12, 2, 11)

_____

The applicable rules of exponents are ...

(a^b)^c = a^(bc)

(ab)^c = (a^c)(b^c)

(a^b)/(a^c) = a^(b-c)