Answer:
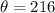
Explanation:
Given
Area of Sector : Area of Circle = 3 : 5
Required
Determine the central angle
The question implies that
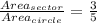
Multiply both sides by 5

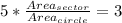
Multiply both sides by Area{circle}
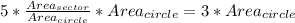
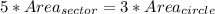
Substitute the areas of sector and circle with their respective formulas;
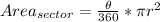
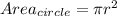
So, we have
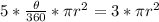
Divide both sides by

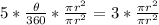
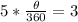
Multiply both sides by 360
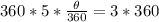
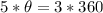
Divide both sides by 5
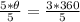
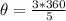
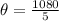
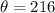
Hence, the central angle is 216 degrees