Question

Find the central angle of a sector of a circle of the area of the sector and the area of the circle are in the proportion of 3:5

Answer 1

`\theta = 216`

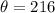
Explanation:

Given

Area of Sector : Area of Circle = 3 : 5

Required

Determine the central angle

The question implies that

`(Area_(sector))/(Area_(circle)) = (3)/(5)`

Multiply both sides by 5

`5 * (Area_(sector))/(Area_(circle)) = (3)/(5) * 5`

`5 * (Area_(sector))/(Area_(circle)) = 3`

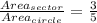
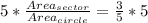
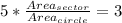
Multiply both sides by Area{circle}

`5 * (Area_(sector))/(Area_(circle)) * Area_(circle) = 3 * Area_(circle)`

`5 * {Area_(sector) = 3 * Area_(circle)`

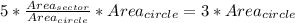
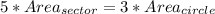
Substitute the areas of sector and circle with their respective formulas;

`Area_(sector) =(\theta)/(360) * \pi r^2`

`Area_(circle) = \pi r^2`

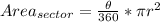
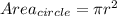
So, we have

`5 * (\theta)/(360) * \pi r^2 = 3 * \pi r^2`

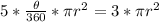
Divide both sides by
`\pi r^2`

`5 * (\theta)/(360) * ( \pi r^2)/(\pi r^2) = 3 * (\pi r^2)/(\pi r^2)`

`5 * (\theta)/(360) = 3`

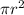
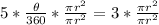
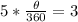
Multiply both sides by 360

`360 * 5 * (\theta)/(360) = 3 * 360`

`5 * \theta = 3 * 360`

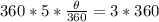
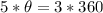
Divide both sides by 5

`(5 * \theta)/(5) = (3 * 360)/(5)`

`\theta = (3 * 360)/(5)`

`\theta = (1080)/(5)`

`\theta = 216`

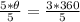
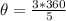
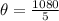
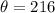
Hence, the central angle is 216 degrees