Question

The manager of a warehouse would like to know how many errors are made when a product's serial number is read by

a bar-code reader. Six samples are collected of the number of scanning errors: 36, 14, 21, 39, 11, and 2 errors, per 1,000
scans each
Just to be sure, the manager has six more samples taken:
33, 45, 34, 17, 1, and 29 errors, per 1,000 scans each
How do the mean and standard deviation change, based on all 12 samples?

Answer 1

14.625

Explanation:

As per the situation the solution of mean and standard deviation change, based on all 12 samples is represented below:-

Mean of all 12 samples is shown below:-

`= (Sum \ of \ all \ the \ observations)/(Total \ number \ of \ observation)`

`= (36+14+21+39+11+2+33+45+34+17+1+29)/(12)`

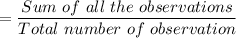
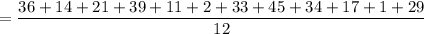
So, the Mean = 23.5

and now,

The Standard deviation of all 12 samples is shown below:-

`= \sqrt{(1)/(12)} (36-23.5)^2+(14-23.5)^2+(21-23.5)^2+(39-23.5)^2+(11-23.5)^2+(2-23.5)^2+(33-23.5)^2+(45-23.5)^2+(34-23.5)^2+(17-23.5)^2+(1-23.5)^2+(29-23.5)^2}]`

`\sigma` = 14.625

Therefore, we used the above equation to reach the answer.