Question

Excell Computers promptly shipped two servers to its biggest client. The company profits RM5,000 on each one of these big systems. The shipping worker randomly selected the system without replacement that were delivered from 15 computers in stock. The system contain 4 refurbished computer, with 11 new computers in the warehouse.

If the client gets two new computers, Excell earns RM10,000 profit. If the client gets a refurbished computer, it’s coming back for replacement and Excell must pay the RM400 shipping fee, with leaves RM9,600 profit. If both computers shipped are refurbished, consequently the client will return both and cancel the order. As a result, Excell will be out any profit and left with RM8,000 in shipping cost. Let X be a random variable for the amount of the profit earned on the order.​

Answer 1

$9215.24

Explanation:

Total Number of Computers=15

Number of New=11

Number of Refurbished Computers=4

• P(New)=11/15
• P(Refurbished)=4/15

`P(NN)=(11)/(15) * (10)/(14) = (11)/(21)\\P(NR)=(11)/(15) * (4)/(14) = (22)/(105)\\P(RN)=(4)/(15) * (11)/(14) = (22)/(105)\\P(RR)=(4)/(15) * (3)/(14) = (2)/(35)`

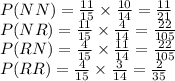
The probability of one new and one refurbished =P(NR)+P(RN)

`=(22)/(105)+ (22)/(105)\\=(44)/(105)`

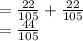
Let X be the amount of profit earned on the purchase. The probability distribution of X is given as:

`\left|\begin{array}c$Profit(X)& NN=\$10000 &NR=\$9600& RR=-\$800\\$P(X)&(11)/(21)&(44)/(105)&(2)/(35)\end{array}\right|`

(b) Expected Profit

`\text{Expected Profit}=\sum X_iP(X_i)\\=(10000 * (11)/(21)) +(9600 * (44)/(105)) + (-800 * (2)/(35))\\=\$9215.24`

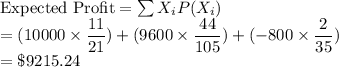
The average profit of the store on the order is $9215.24.