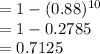Question

intext:"A shipment of 50 inexpensive digital​ watches, including 6 that are​ defective, is sent to a department store. The receiving department selects 10 at random for testing and rejects the whole shipment if 1 or more in the sample are found defective. What is the probability that the shipment will be​ rejected?"

Answer 1

0.7125

Explanation:

The binomial distribution with parameters n and p is the discrete probability distribution of the number of successes (with probability p) in a sequence of n independent events.

The probability of getting exactly x successes in n independent Bernoulli trials =
`n_{C_(x)}(p)^x(1-p)^(n-x)`

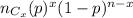
Total number of watches in the shipment = 50

Number of defective watches = 6

Number of selected watches = 10

Let X denotes the number of defective digital watches such that the random variable X follows a binomial distribution with parameters n and p.

So,

Probability of defective watches =
`(X)/(n)=(6)/(50)=0.12`

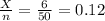
Take n = 10 and p = 0.12

Probability that the shipment will be rejected =
`P(X\geq 1)=1-P(X=0)`

`=1-n_{C_(x)}(p)^x(1-p)^(n-x)\\=1-10_{C_(0)}(0.12)^0(1-0.12)^(10-0)`

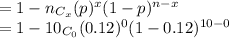
Use
`n_{C_(x)}=(n!)/(x!(n-x)!)`

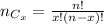
So,

Probability that the shipment will be rejected =
`=1-\left ( (10!)/(0!(10-0)!) \right )(0.88)^(10)`

`=1-(0.88)^(10)\\=1-0.2785\\=0.7125`