Answer:
a) From the empirical rule we know that within 3 deviations from the mean we have 99.7% of the data so then that would be the answer for this case.
b)
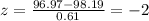
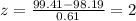
And within 2 deviations from the mean we have 95% of the values.
Explanation:
For this case we know that the distribution of the temperatures have the following parameters:

Part a
From the empirical rule we know that within 3 deviations from the mean we have 99.7% of the data so then that would be the answer for this case.
Part b
We can calculate the number of deviations from the mean with the z score with this formula:
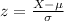
And using this formula we got:
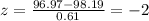
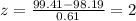
And within 2 deviations from the mean we have 95% of the values.