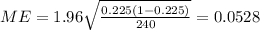Question

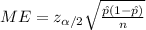
Liam wants to estimate the percentage of people who lease a car. He surveys 240 individuals and finds that 54 lease a car. Find the margin of error for the confidence interval for the population proportion with a 95% confidence level. z0.10 z0.05 z0.025 z0.01 z0.005 1.282 1.645 1.960 2.326 2.576

Answer 1

`ME= z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

The confidence interval is 95% and the significance level is
`\alpha=1-0.95=0.05` and
`\alpha/2 =0.025` and the critical value would be:

`z_(\alpha/2)= 1.96`

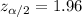
And the margin of error would be:

`ME = 1.96 \sqrt{(0.225 (1-0.225))/(240)}= 0.0528`

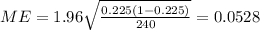
Explanation:

We have the following info given:

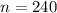`n =240` the sample size selected

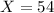`X=54` the number of people who lease a car

`\hat p =(54)/(240)= 0.225` the estimated proportion of people who lease a car

The margin of error is given by:

`ME= z_(\alpha/2) \sqrt{(\hat p(1-\hat p))/(n)}`

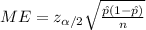
The confidence interval is 95% and the significance level is
`\alpha=1-0.95=0.05` and
`\alpha/2 =0.025` and the critical value would be:

`z_(\alpha/2)= 1.96`

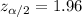
And the margin of error would be:

`ME = 1.96 \sqrt{(0.225 (1-0.225))/(240)}= 0.0528`