Answer:
18.66 ft/s
Explanation:
The distance between you and the elevator is given by:
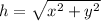
The rate of change for the distance between you and the elevator is given by:
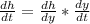
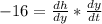
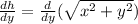
Applying the chain rule:
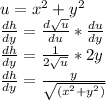
Therefore, at x=300 and y = 500, dy/dt is:
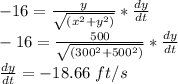
The elevator is descending at 18.66 ft/s.