Question

You are situated 300 feet from the base of Tower Glitz Plaza watching an external elevator descend down the side of the building. At a certain instant the elevator is 500 feet away from you, and its distance from you is decreasing at a rate of 16 ft/sec. How fast is the elevator descending at that instant?

Answer 1

18.66 ft/s

Explanation:

The distance between you and the elevator is given by:

`h=√(x^2+y^2)`

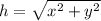
The rate of change for the distance between you and the elevator is given by:

`(dh)/(dt)=(dh)/(dy)*(dy)/(dt)`

`-16=(dh)/(dy)*(dy)/(dt)`

`(dh)/(dy)=(d)/(dy) (√(x^2+y^2))\\`

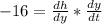
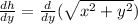
Applying the chain rule:

`u=x^2+y^2\\(dh)/(dy)=(d\sqrt u)/(du) *(du)/(dy)\\(dh)/(dy)=(1)/(2\sqrt u) *2y\\(dh)/(dy)=\frac{y}{\sqrt {(x^2+y^2)}}`

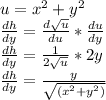
Therefore, at x=300 and y = 500, dy/dt is:

`-16=\frac{y}{\sqrt {(x^2+y^2)}}*(dy)/(dt)\\-16=\frac{500}{\sqrt {(300^2+500^2)}}*(dy)/(dt)\\(dy)/(dt)=-18.66\ ft/s`

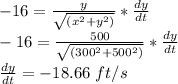
The elevator is descending at 18.66 ft/s.