Question

Which statements are true about circle Q? Select three options. The ratio of the measure of central angle PQR to the measure of the entire circle is One-eighth. The area of the shaded sector is 4 units2. The area of the shaded sector depends on the length of the radius. The area of the shaded sector depends on the area of the circle. The ratio of the area of the shaded sector to the area of the circle is equal to the ratio of the length of the arc to the area of the circle.

Multiple Choice

Answer 1

Answer: 1, 3, 4

Explanation:

Answer 2

- The ratio of the measure of central angle PQR to the measure of the entire circle is One-eighth.

- The area of the shaded sector depends on the length of the radius.

- The area of the shaded sector depends on the area of the circle

Explanation:

Given central angle PQR = 45°

Total angle in a circle = 360°

Ratio of the measure of central angle PQR to the measure of the entire circle is
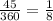`(45)/(360) = (1)/(8)`. This shows ratio that the measure of central angle PQR to the measure of the entire circle is one-eighth.

Area of a sector =
`(\theta)/(360)*\pi r^(2)`

`\theta` = central angle (in degree) = 45°

r = radius of the circle = 6

Area of the sector

`= (45)/(360)*\pi (6)^(2)\\ = (1)/(8)*36 \pi\\ = 4.5\pi units^(2)`

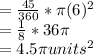
The ratio of the shaded sector is 4.5πunits² not 4units²

From the formula, it can be seen that the ratio of the central angle to that of the circle is multiplied by area of the circle, this shows that area of the shaded sector depends on the length of the radius and the area of the circle.

Since Area of the circle = πr²

Area of the circle = 36πunits²

The ratio of the area of the shaded sector to the area of the circle =
`(4.5\pi )/(36 \pi ) = (1)/(8)`

For length of an arc

`= (45)/(360)*2\pi r\\= (45)/(360)*2\pi (6)\\= (45)/(360)*12 \pi \\= (12\pi )/(8) \\= (3\pi )/(2) units`

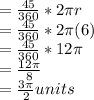
ratio of the length of the arc to the area of the circle =
`((3\pi)/(2) )/(36\pi) = (3)/(72) =(1)/(24)`

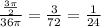
It is therefore seen that the ratio of the area of the shaded sector to the area of the circle IS NOT equal to the ratio of the length of the arc to the area of the circle