Answer:
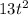 feet higher the stone will travel on the other plant than on Earth.
feet higher the stone will travel on the other plant than on Earth.
Explanation:
Initial velocity of the stone thrown vertically = 79 ft/s
It is given that:
Height attained on a different planet with time
 :
:

Height attained on Earth with time
 :
:
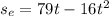
If we have a look at the values of
 , it can be clearly seen that the part
, it can be clearly seen that the part
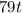 is common in both of them and some values are subtracted from it.
is common in both of them and some values are subtracted from it.
The values subtracted are
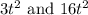 respectively.
respectively.
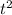 can never be negative because it is time value.
can never be negative because it is time value.
So, coefficient of
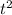 will decide which is larger value that is subtracted from the common part i.e.
will decide which is larger value that is subtracted from the common part i.e.
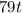 .
.
Clearly,
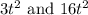 have
have
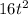 are the larger value, hence
are the larger value, hence
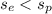 .
.
So, difference between the height obtained:
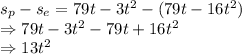
So,
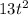 feet higher the stone will travel on the other plant than on Earth.
feet higher the stone will travel on the other plant than on Earth.