Question

In the Journal of Shell and Spatial Structures (December 1963), environmental researcher Vivek Ajmani studied the performance of truss and frame structures subjected to uncertain loads. The load was assumed to have a normal distribution with a mean of 20,000 pounds. Also, the probability that the load is between 10,000 and 30,000 pounds is 0.95. Based on this information, find the standard deviation of the load distribution. Put your answer in three decimal places.

Answer 1

The standard deviation of the load distribution is of 5102.041 pounds.

Explanation:

When the distribution is normal, we use the z-score formula.

In a set with mean
`\mu` and standard deviation
`\sigma`, the zscore of a measure X is given by:

`Z = (X - \mu)/(\sigma)`

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.

In this question, we have that:

`\mu = 20000`

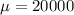
Also, the probability that the load is between 10,000 and 30,000 pounds is 0.95.

10,000 pounds and 30,000 pounds are equidistant from the mean. Due to this, and the probability of 0.95 of having a value in this range, 10000 is the (100-95)/2 = 2.5th percentile and 30000 is the (100+95)/2 = 97.5th percentile. Applying one of them, we find the standard deviation.

30,000 is the 97.5th percentile:

This means that when X = 30000, Z has a pvalue of 0.975. So when X = 30000, Z = 1.96. Then

`Z = (X - \mu)/(\sigma)`

`1.96 = (30000 - 20000)/(\sigma)`

`1.96\sigma = 10000`

`\sigma = (10000)/(1.96)`

`\sigma = 5102.041`

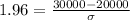
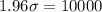
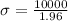
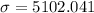
The standard deviation of the load distribution is of 5102.041 pounds.