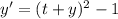
Substitute
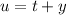 , so that
, so that
 , and
, and

which is separable as
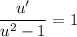
Integrate both sides with respect to
 . For the integral on the left, first split into partial fractions:
. For the integral on the left, first split into partial fractions:
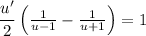
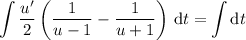
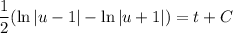
Solve for
 :
:
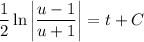

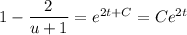
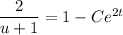
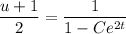

Replace
 and solve for
and solve for
 :
:
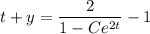
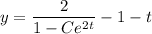
Now use the given initial condition to solve for
 :
:
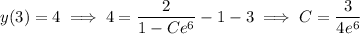
so that the particular solution is
