Answer:
V is not a vector space
Explanation:
Given: V = R be the set of all reals with the operations (a) u + v = uv and (b) a • u = au.
To find: whether V is a vector space or not
Solution:
A vector is a quantity that has both magnitude and direction.
A vector space is a set of all vectors.
According to properties of vector space,
there is a vector 0 (zero vector) such that
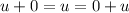
According to the given condition: u + v = uv
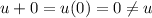
So, there does not exists a zero vector in V such that
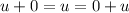
Hence, V is not a vector space.