Question

Let V = R be the set of all reals with the operations (a) u + v = uv and (b) a • u = au. Determine whether V is a vector space or not? Hint: check to see if at least one of the 2 closures or one of the 8 properties fails, then V is NOT a vector space!​

Answer 1

V is not a vector space

Explanation:

Given: V = R be the set of all reals with the operations (a) u + v = uv and (b) a • u = au.

To find: whether V is a vector space or not

Solution:

A vector is a quantity that has both magnitude and direction.

A vector space is a set of all vectors.

According to properties of vector space,

there is a vector 0 (zero vector) such that
`u+0=u=0+u`

According to the given condition: u + v = uv

`u+0=u(0)=0\\eq u`

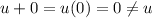
So, there does not exists a zero vector in V such that
`u+0=u=0+u`

Hence, V is not a vector space.