Question

The volume of this cone is 65.94 cubic feet. What is the radius of this cone? Use ​ ≈ 3.14 and round your answer to the nearest hundredth.

Answer 1

In terms of h

radius = 3√7)√ h

Explanation:

`volume \: = 65.94 \\ \pi = 3.14 \\ radius =`

`v = (1)/(3) \pi {r}^(2) h \\ 65.94 = (1)/(3) * 3.14 * {r}^(2) * h \\ 65.94 * 3 = 1 * 3.14 * {r}^(2) h`

`197.82 = 3.14 {r}^(2) h \\ divide \: both \: sides \: of \: the \: equation \: \\ by3.14 h\\ (197.82)/(3.14h) = \frac{3.14 {r}^(2)h }{3.14h}`

`(63)/(h) = {r}^(2) \\ square \: root \: both \: sides \\ \sqrt{ (63)/(h) } = \sqrt{ {r}^(2) } \\ r \: = (3 √(7) )/( √(h) )`

Answer 2

In terms of h, the radius of the cone is
`(3√(7) )/(√(h) )`

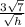
Explanation:

The formula for finding the volume of a cone is

`Volume(V) = (1)/(3) \pi r^(2) h`

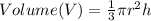
Make r the subject of formula in the equation above

`3V = \pi r^(2) h`

`(3V)/(\pi h ) = (\pi r^(2) h)/(\pi h)`

`r^(2) = (3V)/(\pi h)`

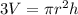
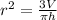
Take the square root of both sides of the equation

`\sqrt{r^(2) } = \sqrt{(3V)/(\pi h) }`

`r = \sqrt{(3V)/(\pi h) }`

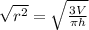
Putting in the values given,

`r = \sqrt{(3 * 65.94 )/(3.14h) }`

`r = \sqrt{(3 * 21 )/(h)}`

`r = \sqrt{(63 )/(h) }`

`r = \sqrt{(9 * 7)/(h) }`

`r = (3√(7) )/(√(h) )`

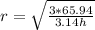
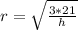
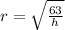
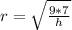
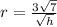
Hope this helps :))