Answer:
The mean and standard deviation of the combined distribution is 16 and 7.192 respectively.
Explanation:
We have given that a distribution consists of three components with frequencies 200, 250, and 300 having means 25, 10, and 15 and standard deviations 3, 4, and 5 respectively.
And we have to find the mean and standard deviation of the combined distribution.
Firstly let us represent some symbols;
 = 200
= 200
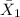 = 25
= 25
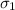 = 3
= 3
 = 250
= 250
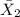 = 10
= 10
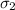 = 4
= 4
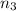 = 300
= 300
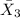 = 15
= 15
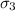 = 5
= 5
Here,
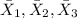 represent the means and
represent the means and
 represent the standard deviations.
represent the standard deviations.
Now, as we know that Mean of the combined distribution is given by;
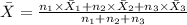
Putting the above values in the formula we get;
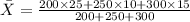
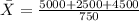
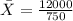 = 16
= 16
Similarly, the formula for combined standard deviation is given by;
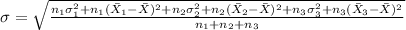
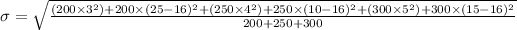
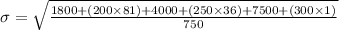
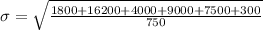
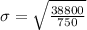 = 7.192
= 7.192
Hence, the mean and standard deviation of the combined distribution is 16 and 7.192 respectively.