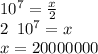Question

60 POINTS Explain the process and solve a logarithmic equation. log x + log 8 – 2log 4 = 7.

Answer 1

`x = 20000000`

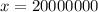
Explanation:

Recall the power property of logarithms which states:

`log(a^n)=n\,\,log(a)`

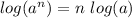
to re-write
`2\,log(4)=log(4^2)=log(16)`

and then use the product and quotient rules of logarithms:

`log (A*B)=log(A)+log(B)`

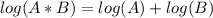
and

`log ((A)/(B) )=log(A)-log(B)`

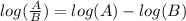
to rewrite the combination of logarithms on the left of the equal sign as a single logarithm:

`log(x)+log(8)-2\,\,log(4)=7\\log(x)+log(8)-log(16)=7\\log((8\,x)/(16)) =7\\log((x)/(2)) =7`

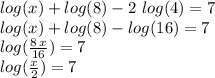
and now re-write this equation in exponent form to get rid of the logarithm:

`10^7=(x)/(2) \\2\,\,\,10^7 = x\\x = 20000000`