Question

Find the five-number summary for the data.

{238, 213, 223, 212, 225, 233, 230, 239, 223, 207, 219,
217, 234, 204, 212, 242}
A. 204, 212.5, 223, 233.5, 242
B. 204, 212, 223, 233, 239
OC. 204, 212, 219, 233, 242
OD. 207, 212, 223, 234, 239

Answer 1

The correct option is A. 204, 212.5, 223, 233.5, 242.

Explanation:

The five number summary of a data set is:

1. Minimum
2. First Quartile
3. Median
4. Third Quartile
5. Maximum.

The data provided, in ascending order is:

S = {204 , 207 , 212 , 212 , 213 , 217 , 219 , 223 , 223 , 225 , 230 , 233 , 234 , 238 , 239 , 242}

There are a total of 16 values in the data set.

The minimum value is,

Minimum = 204

The first quartile is the median value of the first half of the data.

The first half of the data is:

S₁ = {204 , 207 , 212 , 212 , 213 , 217 , 219 , 223 }

The median for even number of observations is the mean of the middle two values.

`\text{Q}_(1)=(4^(th)+5^(th))/(2)=(212+213)/(2)=212.5`

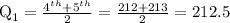
The first quartile is 212.5.

The median for even number of observations is the mean of the middle two values.

`\text{Median}=(8^(th)+9^(th))/(2)=(223+223)/(2)=223`

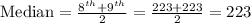
The median of the data is 223.

The third quartile is the median value of the second half of the data.

The first half of the data is:

S₂ = {223 , 225 , 230 , 233 , 234 , 238 , 239 , 242}

The median for even number of observations is the mean of the middle two values.

`\text{Q}_(3)=(12^(th)+13^(th))/(2)=(233+234)/(2)=233.5`

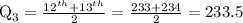
The third quartile is 233.5.

The maximum value is,

Maximum = 242