Question

Of 585 samples of seafood purchased from various kinds of food stores in different regions of a country and genetically compared to standard gene fragments that can identify the​ species, 19​% were mislabeled. ​a) Construct a 99​% confidence interval for the proportion of all seafood sold in the country that is mislabeled or misidentified. ​b) Explain what your confidence interval says about seafood sold in the country. ​c) A government spokesperson claimed that the sample size was too​ small, relative to the billions of pieces of seafood sold each​ year, to generalize. Is this criticism​ valid? ​a) What is the 99​% confidence​ interval? The 99​% confidence interval is from nothing​% to nothing​%. ​(Round to one decimal place as​ needed.)

Answer 1

a) The 99% confidence interval is from 14.8% to 23.2%.

b) The confidence interval tells us that the true proportion of mislabeled is within 14.8% and 23.2%, with a 99% confidence. In other words, if we take samples of the same size, 99% of the samples will have a proportion within 0.148 and 0.232.

c) The confidence interval calculation take into account the sample size, so the width (or precision) of the interval depends on the sample size.

The only criticism that could be analyzed is to see if the sample is representative of the population.

Explanation:

a) We have to calculate a 99% confidence interval for the proportion.

The sample proportion is p=0.19.

The standard error of the proportion is:

`\sigma_p=\sqrt{(p(1-p))/(n)}=\sqrt{(0.19*0.81)/(585)}\\\\\\ \sigma_p=√(0.000263)=0.016`

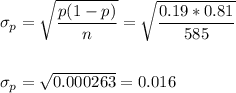
The critical z-value for a 99% confidence interval is z=2.576.

The margin of error (MOE) can be calculated as:

`MOE=z\cdot \sigma_p=2.576 \cdot 0.02=0.042`

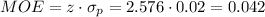
Then, the lower and upper bounds of the confidence interval are:

`LL=p-z \cdot \sigma_p = 0.19-0.042=0.148\\\\UL=p+z \cdot \sigma_p = 0.19+0.042=0.232`

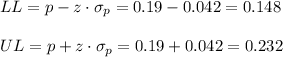
The 99% confidence interval for the population proportion is (0.148, 0.232).