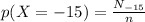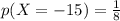Question

Suppose that the genders of the three children of a certain family are soon to be revealed. Outcomes are thus triples of "girls" (g) and "boys" (b), which we write gbg, bbb, etc. For each outcome, let R be the random variable counting the number of girls in each outcome. For example, if the outcome is gbb, then R9gbb)=1. Suppose that the random variable X is defined in terms of R as follows: X=2R^2-4R-2. The values of X are thus:

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

Value x of X -3 -7 -15

`P_X (x)`
`(1)/(2)`
`(3)/(8)`
`(1)/(8)`

Explanation:

From the question we are told that

The values of X are
`X = -3 , -7 , -15`

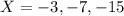
The total number of outcomes is n = 8

The probability distribution function of X is evaluated as follow

`p(X = -3 ) = (N_(-3))/(n)`

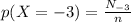
Where
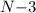`N{-3}` is the number of time X = -3 occurred and from the table the value is
`N _(-3) = 4`

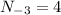
Therefore

`p(X = -3 ) = (4)/(8)`

`p(X = -3 ) = (1)/(2)`

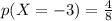
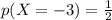
Now

`p(X = -7 ) = (N_(-7))/(n)`

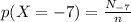
Where
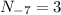`N_(-7) = 3` from table

So

`p(X = -7 ) = (3)/(8)`

Also

`p(X = -15 ) = (N_(-15))/(n)`

`p(X = -15 ) = (1)/(8)`