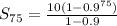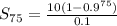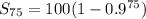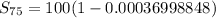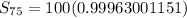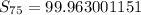Question:
The geometric sequence ; is defined by the formula:
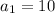 ;
;
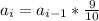 Find the sum of the first 75 terms in the sequence .
Find the sum of the first 75 terms in the sequence .
Answer:
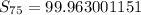
Explanation:
Given
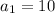
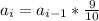
Required
Find the sum of 75 terms
Given that the sequence is geometric;
First, the common ratio has to be calculated;
The common ratio is defined as follows;

Let

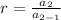
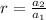
So,
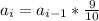 becomes
becomes
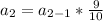
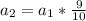
Divide through by

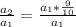
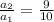
Recall that
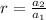
So,
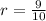
Given that r < 1;
The sum of n terms is calculated as thus;
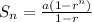
To calculate the sum of the first 75 terms, we have the following parameters
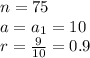
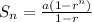 becomes
becomes