Answer:
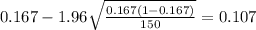
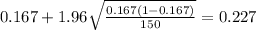
And the 95% confidence interval would be given (0.107;0.227).
Explanation:
Information given
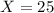 number of trees with signs of disease
number of trees with signs of disease
 the sample selected
the sample selected
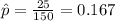 the proportion of trees with signs of disease
the proportion of trees with signs of disease
The confidence interval for the true proportion would be given by this formula
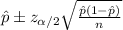
For the 95% confidence interval the significance is
 and
and
 , and the critical value would be
, and the critical value would be
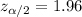
And replacing we got:
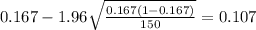
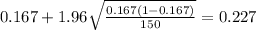
And the 95% confidence interval would be given (0.107;0.227).