Question

The weights of a certain brand of candies are normally distributed with a mean weight of 0.8548 g and a standard deviation of 0.0512 g. A sample of these candies came from a package containing 444 ​candies, and the package label stated that the net weight is 379.3 g.​ (If every package has 444 ​candies, the mean weight of the candies must exceed 379.3/444 = 0.8543 g for the net contents to weigh at least 379.3 ​g.)

(a) If 1 candy is randomly selected, find the probability that it weighs more than 0.8542g. (Round to four decimal places as needed.)


(b) If 447 candies are randomly selected find the probability that their mean weight is at least 0.8542 g. (Round to four decimal places as needed.)


(c) Given these results does it seem that the candy company is providing consumers with the amount claimed on the label?

Answer 1

a) 0.5047

b) 0.5978

c) Yes

Explanation:

Given:

Mean, u = 0.8548

Standard deviation = 0.0512

Sample mean, X' = 0.8542

a) If 1 candy is randomly selected, the probability that it weighs more than 0.8542 would be:

`z = (X' - u)/(\sigma) = (0.8542 - 0.8548)/(0.0512) = -0.0117`

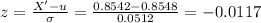
From standard normal table, NORMSTD(-0.0117) = 0.4953

P(z > -0.0117) = 1 - 0.4953 = 0.5047

Probability = 0.5047

b) If 447 candies are randomly selected the probability that their mean weight is at least 0.8542:

Here, we are to find the probability that the men weight is greater or equal to 0.8542

`z = (X' - u)/(\sigma / √(n)) = (0.8542 - 0.8548)/(0.0512/ √(447)) = -0.24776`

From standard normal table, NORMSTD(-0.24776) = 0.40216

P(z > -0.0117) = 1 - 0.40216 = 0.5978

Probability = 0.5978

c) Yes, it seems the candy company is providing consumers with the amount claimed on the label, because the probability of getting a sample mean of 0.8542 or greater when 447 candies are selected is not exceptionally small