Question

The angle measures associated with which set of ordered pairs share the same reference angle? (Negative StartFraction StartRoot 3 EndRoot Over 2 EndFraction , negative one-half), (negative one-half, Negative StartFraction StartRoot 3 EndRoot Over 2 EndFraction) (one-half, Negative StartFraction StartRoot 3 EndRoot Over 2 EndFraction), (Negative StartFraction StartRoot 3 EndRoot Over 2 EndFraction, one-half) (Negative one-half, negative StartFraction StartRoot 3 EndRoot Over 2 EndFraction), (One-half, StartFraction StartRoot 3 EndRoot Over 2 EndFraction) (StartFraction StartRoot 3 EndRoot Over 2 EndFraction, one-half), (one-half, StartFraction StartRoot 3 EndRoot Over 2 EndFraction)

Answer 1

C

Explanation:

Answer 2

`(C)\left(-(1 )/(2),-(√(3) )/(2) \right)$ and \left((1 )/(2),(√(3) )/(2) \right)`

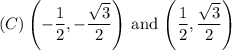
Explanation:

The reference angle is the angle that the given angle makes with the x-axis.

For an ordered pair to share the same reference angle, the x and y coordinates must be the same or a factor of each other.

From the given options:

`(A)\left(-(√(3) )/(2) ,-(1 )/(2)\right)$ and \left(-(1 )/(2),-(√(3) )/(2) \right)\\\\(B)\left((1 )/(2),-(√(3) )/(2) \right)$ and \left(-(√(3) )/(2), (1 )/(2)\right)\\\\(C)\left(-(1 )/(2),-(√(3) )/(2) \right)$ and \left((1 )/(2),(√(3) )/(2) \right)\\\\(D)\left((√(3) )/(2),(1 )/(2) \right)$ and \left((1 )/(2),(√(3) )/(2) \right)`

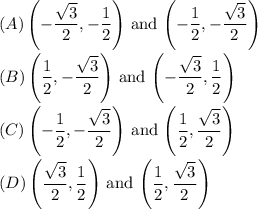
We observe that only the pair in option C has the same x and y coordinate with the second set of points being a negative factor of the first term. Therefore, they have the same reference angle.