Answer:
a. 46.15%
b. 261.73 kg/s
c. 54.79 kW/K
Step-by-step explanation:
a. State 1
The parameters given are;
T₁ = 560°C
P₁ = 12 MPa = 120 bar
Therefore;
h₁ = 3507.41 kJ/kg, s₁ = 6.6864 kJ/(kg·K)
State 2
p₂ = 1 MPa = 10 bar
s₂ = s₁ = 6.6864 kJ/(kg·K)
h₂ = (6.6864 - 6.6426)÷(6.6955 - 6.6426)×(2828.27 - 2803.52) + 2803.52
= (0.0438 ÷ 0.0529) × 24.75 = 2824.01 kJ/kg
State 3
p₃ = 6 kPa = 0.06 bar
s₃ = s₁ = 6.6864 kJ/(kg·K)
sg = 8.3291 kJ/(kg·K)
sf = 0.52087 kJ/(kg·K)
x = s₃/sfg = (6.6864- 0.52087)/(8.3291 - 0.52087) = 0.7896
(h₃ - 151.494)/2415.17 = 0.7896
∴ h₃ = 2058.56 kJ/kg
State 4
Saturated liquid state
p₄ = 0.06 bar= 6000 Pa, h₄ = 151.494 kJ/kg, s₄ = 0.52087 kJ/(kg·K)
State 5
Open feed-water heater
p₅ = p₂ = 1 MPa = 10 bar = 1000000 Pa
s₄ = s₅ = 0.52087 kJ/(kg·K)
h₅ = h₄ + work done by the pump on the saturated liquid
∴ h₅ = h₄ + v₄ × (p₅ - p₄)
h₅ = 151.494 + 0.00100645 × (1000000 - 6000)/1000 = 152.4944113 kJ/kg
Step 6
Saturated liquid state
p₆ = 1 MPa = 10 bar
h₆ = 762.683 kJ/kg
s₆ = 2.1384 kJ/(kg·K)
v₆ = 0.00112723 m³/kg
Step 7
p₇ = p₁ = 12 MPa = 120 bar
s₇ = s₆ = 2.1384 kJ/(kg·K)
h₇ = h₆ + v₆ × (p₇ - p₆)
h₇ = 762.683 + 0.00112723 * (12 - 1) * 1000 = 775.08253 kJ/kg
The fraction of flow extracted at the second stage, y, is given as follows
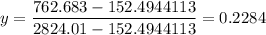
The turbine control volume is given as follows;
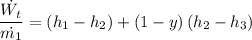
= (3507.41 - 2824.01) + (1 - 0.22840)*(2824.01 - 2058.56) = 1274.02122 kJ/kg
For the pumps, we have;
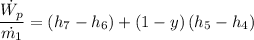
= (775.08253 - 762.683) + (1 - 0.22840)*(152.4944113 - 151.494)
= 13.17 kJ/kg
For the working fluid that flows through the steam generator, we have;
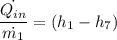
= 3507.41 - 775.08253 = 2732.32747 kJ/kg
The thermal efficiency, η, is given as follows;
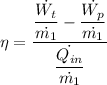
η = (1274.02122 - 13.17)/2732.32747 = 0.4615 which is 46.15%
(762.683 - 152.4944113)/(2824.01 - 152.4944113)
b. The mass flow rate,
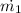 , into the first turbine stage is given as follows;
, into the first turbine stage is given as follows;
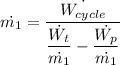
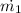 = 330 *1000/(1274.02122 - 13.17) = 261.73 kg/s
= 330 *1000/(1274.02122 - 13.17) = 261.73 kg/s
c. From the entropy rate balance of the steady state form, we have;
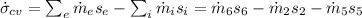
![\dot{\sigma }_(cv) = \dot{m}_(6) \left [s_(6) - ys_(2) - (1 - y)s_(5) \right ]](https://img.qammunity.org/2021/formulas/engineering/college/52yl1aeflwugjq30l1h4snkqgh0p005m5f.png)
= 261.73 * (2.1384 - 0.2284*6.6864 - (1 - 0.2284)*0.52087 = 54.79 kW/K