Answer:
The time elapsed at the spacecraft’s frame is less that the time elapsed at earth's frame
Step-by-step explanation:
From the question we are told that
The distance between earth and Retah is
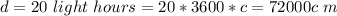
Here c is the peed of light with value

The time taken to reach Retah from earth is
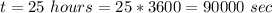
The velocity of the spacecraft is mathematically evaluated as
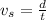
substituting values
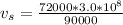
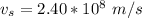
The time elapsed in the spacecraft’s frame is mathematically evaluated as
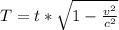
substituting value
![T = 90000 * \sqrt{ 1 - ([2.4*10^(8)]^2)/([3.0*10^(8)]^2) }](https://img.qammunity.org/2021/formulas/physics/college/uk271bd89je6jpst8p09n3i20r9k9ds0bm.png)
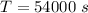
=>
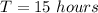
So The time elapsed at the spacecraft’s frame is less that the time elapsed at earth's frame