Question

A yet-to-be-built spacecraft starts from Earth moving at constant speed to the yet-tobe-discovered planet Retah, which is 20 lighthours away from Earth. It takes 25 h (according to an Earth observer) for a spacecraft to reach this planet. Assuming that the clocks are synchronized at the beginning of the journey, compare the time elapsed in the spacecraft’s frame for this one-way journey with the time elapsed as measured by an Earth-based clock.

Answer 1

The time elapsed at the spacecraft’s frame is less that the time elapsed at earth's frame

Step-by-step explanation:

From the question we are told that

The distance between earth and Retah is
`d = 20 \ light \ hours = 20 * 3600 * c = 72000c \ m`

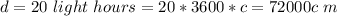
Here c is the peed of light with value
`c = 3.0*10^8 m/s`

The time taken to reach Retah from earth is
`t = 25 \ hours = 25 * 3600 =90000 \ sec`

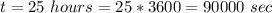
The velocity of the spacecraft is mathematically evaluated as

`v_s = (d )/(t)`

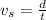
substituting values

`v_s = (72000 * 3.0*10^(8) )/(90000)`

`v_s = 2.40*10^(8) \ m/s`

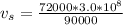
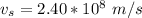
The time elapsed in the spacecraft’s frame is mathematically evaluated as

`T = t * \sqrt{ 1 - (v^2)/(c^2) }`

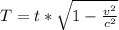
substituting value

`T = 90000 * \sqrt{ 1 - ([2.4*10^(8)]^2)/([3.0*10^(8)]^2) }`

`T = 54000 \ s`

=>
`T = 15 \ hours`

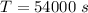
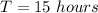
So The time elapsed at the spacecraft’s frame is less that the time elapsed at earth's frame