Answer:
The answer to this question can be described as follows:
-5 with multiplicity 3
9 with multiplicity 2
-1 with multiplicity 1
Explanation:
Given:
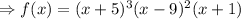
Solve the above equation:
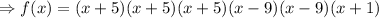
The roots of the polynomial are as follows:
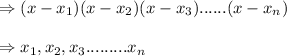
That's why the roots are:
5 with multiplicity 3
9 with multiplicity 2
-1 with multiplicity 1