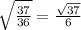Question

show that the equation 3x2 + 3y2 + 6x-y= 0 represents a circle and find the centre and radius of the circle​

Answer 1

Center of the circle:
`(-1,(1)/(6))`

Radius of the circle:
`(√(37) )/(6)`

Explanation:

Let's start by dividing both sides of the equation by the factor "3" so we simplify our next step of completing squares for x and for y:

`3x^2+3y^2+6x-y=0\\x^2+y^2+2x-(1)/(3) y=0`

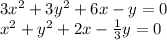
Now we work on completing the squares for the expression on x and for the expression on y separately, so we group together the terms in "x" and then the terms in "y":

`x^2+y^2+2x-(1)/(3) y=0\\( x^2+2x ) + (y^2-(1)/(3) y)=0`

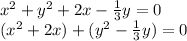
Let's find what number we need to add to both sides of the equation to complete the square of the group on the variable "x":

`( x^2+2x ) = 0\\x^2+2x+1=1\\(x+1)^2=1`

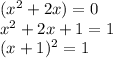
So, we need to add "1" to both sides in order to complete the square in "x".

Now let's work on a similar fashion to find what number we need to add on both sides to complete the square for the group on y":

`(y^2-(1)/(3) y)=0\\y^2-(1)/(3) y+(1)/(36) =(1)/(36)\\(y-(1)/(6) )^2=(1)/(36)`

Therefore, we need to add "
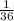`(1)/(36)`" to both sides to complete the square for the y-variable.

This means we need to add a total of
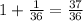`1 + (1)/(36) = (37)/(36)` to both sides of the initial equation in order to complete the square for both variables:

`x^2+y^2+2x-(1)/(3) y=0\\x^2+y^2+2x-(1)/(3) y+(37)/(36) =(37)/(36) \\(x+1)^2+(y-(1)/(6) )^2=(37)/(36)`

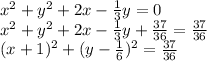
Now recall that the right hand side of this expression for the equation of a circle contains the square of the circle's radius, based on the general form for the equation of a circle of center
`(x_0,y_0)` and radius R:

`(x-x_0)^2+(y-y_0)^2=R^2`

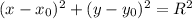
So our equation that can be written as:

`(x+1)^2+(y-(1)/(6) )^2=(\sqrt{(37)/(36)} )^2`

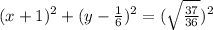
corresponds to a circle centered at
`(-1,(1)/(6))` , and with radius
`\sqrt{(37)/(36)}=(√(37) )/(6)`