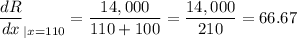Answer:
The change in revenue from the sale of one more doghouse if 110 doghouses have already been sold is dR/dx=66.67 $/doghouse.
Explanation:
We have a revenue function that is:
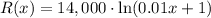
We have to approximate the change in revenue from the sale of one more doghouse, if 110 doghouses have already been sold.
That is the marginal revenue at x=110.
The marginal revenue is expressed as the first derivative of the revenue.
Then, we calculate the derivative of R:
![(dR)/(dx)=(d)/(dx)[14,000\cdot \text{ln}(0.01x+1)]\\\\\\(dR)/(dx)=14,000(d)/(dx)[\text{ln}(0.01x+1)]\\\\\\(dR)/(dx)=14,000\cdot(1)/(0.01x+1)\cdot (d)/(dx)(0.01x+1)\\\\\\(dR)/(dx)=14,000\cdot(1)/(0.01x+1)\cdot 0.01\\\\\\(dR)/(dx)=(14,000)/(x+100)](https://img.qammunity.org/2021/formulas/mathematics/college/mhftp4pl9haugb65t504cbbidvb9kzhb2b.png)
We then evaluate this marginal revenue at point x=110: