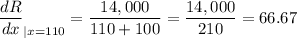Question

A company estimates that the revenue (in dollars) from the sale of x doghouses is given by R(x)=14,000ln(0.01x+1). Use the differential to approximate the change in revenue fro the sale of one more doghouse if 110 doghouses have already been sold. (Round to nearest cent as needed)

Answer 1

The change in revenue from the sale of one more doghouse if 110 doghouses have already been sold is dR/dx=66.67 $/doghouse.

Explanation:

We have a revenue function that is:

`R(x)=14,000\cdot \text{ln}(0.01x+1)`

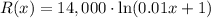
We have to approximate the change in revenue from the sale of one more doghouse, if 110 doghouses have already been sold.

That is the marginal revenue at x=110.

The marginal revenue is expressed as the first derivative of the revenue.

Then, we calculate the derivative of R:

`(dR)/(dx)=(d)/(dx)[14,000\cdot \text{ln}(0.01x+1)]\\\\\\(dR)/(dx)=14,000(d)/(dx)[\text{ln}(0.01x+1)]\\\\\\(dR)/(dx)=14,000\cdot(1)/(0.01x+1)\cdot (d)/(dx)(0.01x+1)\\\\\\(dR)/(dx)=14,000\cdot(1)/(0.01x+1)\cdot 0.01\\\\\\(dR)/(dx)=(14,000)/(x+100)`

We then evaluate this marginal revenue at point x=110:

`(dR)/(dx)_(|x=110)=(14,000)/(110+100)=(14,000)/(210)=66.67`