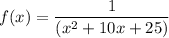Answer:
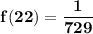
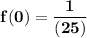
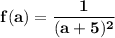
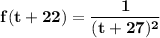
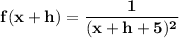
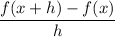 =
=
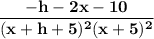
Explanation:
The mathematical interpretation of the A function f is given by
f(x)equals=StartFraction 1 Over left parenthesis x plus 5 right parenthesis squared End Fraction 1(x+5)2 is :
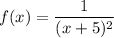
So; we are ask to find the following:
a)
f(22) ; i.e what is the function when x = 22
So replacing x = 22 into the above function; we have:
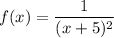
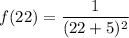
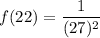
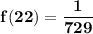
f(0) : i.e what is the function when x = 0
So replacing x = 0 into the given function; we have:
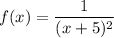
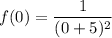
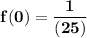
f(a) : i.e what is the function when x = a
So replacing x = a into the given function; we have:
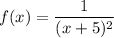
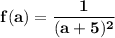
f(tplus+22), i.e what is the function when x = t+22
So replacing x = t+22 into the given function; we have:
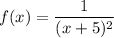
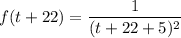
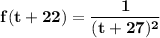
f(xplus+h), i.e what is the function when x =x+h
So replacing x = x+h into the given function; we have:
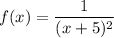
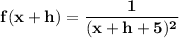
Similarly; another function is given as :
Start Fraction f left parenthesis x plus h right parenthesis minus f left parenthesis x right parenthesis Over h End Fraction f(x+h)-f(x)h.
Mathematically the above function can be expressed as:
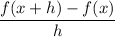
where ;
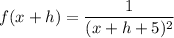 and
and
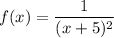
So;
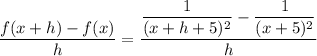
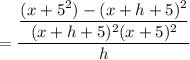
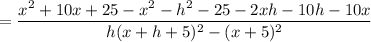
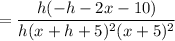
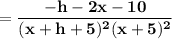
b) Note that f could also be given by
f(x)equals=StartFraction 1 Over x squared plus 10 x plus 25 EndFraction
1×2+10x+25
Explain what this does to an input number x.
The mathematical expression of the function is:
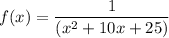
the input = x ; so 5 is added to the i.e x+ 5;
After that the square of the entity (x+5) is taken giving rise to (x+5)²
then the reciprocal of the function is taken ; which now becomes:
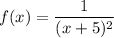
If we expand the quadratic expression in the bracket; we have:
x being multiplied by the square ² which = x²
then x is multiplied by the addition of (5+5 )x to give 10x
Finally 5 is multiplied by the square ² which = 5² = 25
After the addition of all this three together ; the reciprocal was taken to get: