Question

A function f is given by

f(x)equals=StartFraction 1 Over left parenthesis x plus 5 right parenthesis squared End Fraction 1(x+5)2.
This function takes a numbe x, adds
55,
squares the result, and takes the reciprocal of that result.
a) Find
f(22),
f(0), f(a),
f(tplus+22),
f(xplus+h), and
Start Fraction f left parenthesis x plus h right parenthesis minus f left parenthesis x right parenthesis Over h End Fraction f(x+h)-f(x)h.
b) Note that f could also be given by
f(x)equals=StartFraction 1 Over x squared plus 10 x plus 25 EndFraction
1×2+10x+25
Explain what this does to an input number x.

Answer 1

`\mathbf{f(22) = (1)/(729)}`

`\mathbf{f(0) = (1)/((25))}`

`\mathbf {f(a) = (1)/((a+5)^2)}}`

`\mathbf{f(t+22) = (1)/((t+27)^2)}`

`\mathbf{f(x+h) = (1)/((x+h+5)^2)}`

`(f(x+h)-f(x))/(h)`=
`\mathbf{ (-h-2x-10)/((x+h+5)^2(x+5)^2)}`

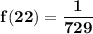
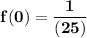
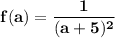
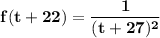
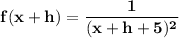
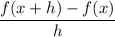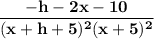
Explanation:

The mathematical interpretation of the A function f is given by

f(x)equals=StartFraction 1 Over left parenthesis x plus 5 right parenthesis squared End Fraction 1(x+5)2 is :

`f(x) = (1)/((x+5)^2)`

So; we are ask to find the following:

a)

f(22) ; i.e what is the function when x = 22

So replacing x = 22 into the above function; we have:

`f(x) = (1)/((x+5)^2)`

`f(22) = (1)/((22+5)^2)`

`f(22) = (1)/((27)^2)`

`\mathbf{f(22) = (1)/(729)}`

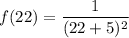
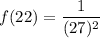
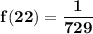
f(0) : i.e what is the function when x = 0

So replacing x = 0 into the given function; we have:

`f(x) = (1)/((x+5)^2)`

`f(0) = (1)/((0+5)^2)`

`\mathbf{f(0) = (1)/((25))}`

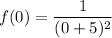
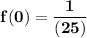
f(a) : i.e what is the function when x = a

So replacing x = a into the given function; we have:

`f(x) = (1)/((x+5)^2)`

`\mathbf {f(a) = (1)/((a+5)^2)}}`

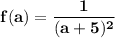
f(tplus+22), i.e what is the function when x = t+22

So replacing x = t+22 into the given function; we have:

`f(x) = (1)/((x+5)^2)`

`f(t+22) = (1)/((t+22+5)^2)`

`\mathbf{f(t+22) = (1)/((t+27)^2)}`

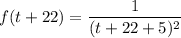
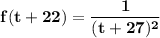
f(xplus+h), i.e what is the function when x =x+h

So replacing x = x+h into the given function; we have:

`f(x) = (1)/((x+5)^2)`

`\mathbf{f(x+h) = (1)/((x+h+5)^2)}`

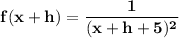
Similarly; another function is given as :

Start Fraction f left parenthesis x plus h right parenthesis minus f left parenthesis x right parenthesis Over h End Fraction f(x+h)-f(x)h.

Mathematically the above function can be expressed as:

`(f(x+h)-f(x))/(h)`

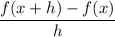
where ;

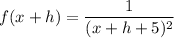`f(x+h) = (1)/((x+h+5)^2)` and
`f(x) = (1)/((x+5)^2)`

So;

`(f(x+h)-f(x))/(h) = ((1)/((x+h+5)^2) -(1)/((x+5)^2) )/(h)`

`=( ((x+5^2)-(x+h+5)^2)/((x+h+5)^2(x+5)^2) )/(h)`

`= (x^2+10x +25-x^2-h^2-25-2xh-10h -10x)/(h(x+h+5)^2-(x+5)^2)`

`= (h(-h-2x-10))/(h(x+h+5)^2(x+5)^2)`

`=\mathbf{ (-h-2x-10)/((x+h+5)^2(x+5)^2)}`

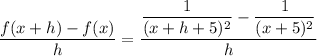
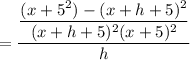
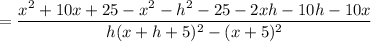
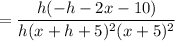
b) Note that f could also be given by

f(x)equals=StartFraction 1 Over x squared plus 10 x plus 25 EndFraction

1×2+10x+25

Explain what this does to an input number x.

The mathematical expression of the function is:

`f(x) = (1)/((x^2+10x + 25))`

the input = x ; so 5 is added to the i.e x+ 5;

After that the square of the entity (x+5) is taken giving rise to (x+5)²

then the reciprocal of the function is taken ; which now becomes:

`f(x) = (1)/((x+5)^2)`

If we expand the quadratic expression in the bracket; we have:

x being multiplied by the square ² which = x²

then x is multiplied by the addition of (5+5 )x to give 10x

Finally 5 is multiplied by the square ² which = 5² = 25

After the addition of all this three together ; the reciprocal was taken to get:

`f(x) = (1)/((x^2+10x + 25))`