Question

A DEF is a right triangle.

Answer 1

The Pythagorean Theorem states that in a right triangle,
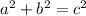`a^(2) + b^(2) = c^(2)`, where a and b are the legs and c is the hypotenuse.

Plugging in this formula, we can identify if DEF is a right triangle.

`25^(2) +27^(2) = c^(2)`

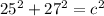
The first step is to plug in our known values.

`625 + 729 = c^(2)`

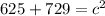
Next, we'll square both values available.

`1354 = c^(2)`

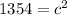
From there, we'll add the values together.

`36.7967.. = c`

Finally, we'll find the square root of our value to get c.

Since our answer is ~36, and the value we're given for the hypotenuse is 48, this is not a right triangle since the values aren't the same.

Therefore, the answer is False.

Hope this helped! :)

Answer 2

The statement is false because ΔDEF is not a right triangle.

Explanation:

We can figure out if this triangle is a right triangle by using the Pythagorean Theorem. The Pythagorean Theorem is a² + b² = c².

a = 26

b = 27

c = 48

Now, let's plug these numbers into the formula.

(26)² + (27)² = (48)²

676 + 729 = 2304

1405 = 2304

1405 does not equal to 2304.

So, ΔDEF is not a right triangle.