Answer:
The ball is at a maximum height when t = 0.125s.
Explanation:
Vertex of a quadratic function:
Suppose we have a quadratic function in the following format:
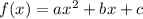
It's vertex is the point
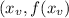
In which

If a<0, the vertex is a maximum point, that is, the maximum value happens at
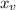 , and it's value is
, and it's value is
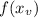
In this question:
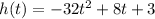
So
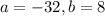
When is the ball at a maximum height
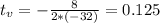
The ball is at a maximum height when t = 0.125s.