Question

The height of a ball above the ground as a function of time is given by the function h(t)= -32t^2+8t+3 where h is the height of the ball in feet and t is the time in seconds. When is the ball at a maximum height

Answer 1

The ball is at a maximum height when t = 0.125s.

Explanation:

Vertex of a quadratic function:

Suppose we have a quadratic function in the following format:

`f(x) = ax^(2) + bx + c`

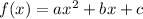
It's vertex is the point
`(x_(v), f(x_(v))`

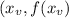
In which

`x_(v) = -(b)/(2a)`

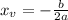
If a<0, the vertex is a maximum point, that is, the maximum value happens at
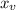`x_(v)`, and it's value is
`f(x_(v))`

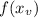
In this question:

`h(t) = -32t^(2) + 8t + 3`

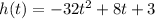
So
`a = -32, b = 8`

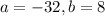
When is the ball at a maximum height

`t_(v) = -(8)/(2*(-32)) = 0.125`

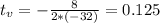
The ball is at a maximum height when t = 0.125s.