Question

In a large population, 57 % of the people have been vaccinated. If 3 people are randomly selected, what is the probability that AT LEAST ONE of them has been vaccinated?

Answer 1

The probability that AT LEAST ONE of them has been vaccinated

P( X ≥1) = 0.920493

Explanation:

Step(i):-

Given 57 % of the people have been vaccinated

p = 57% =0.57

q = 1-p =1-0.57 = 0.43

n = 3

`P(X=r) = n_{C_(r) } p^(r) q^(n-r)`

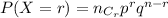
Step(ii):-

The probability that AT LEAST ONE of them has been vaccinated

P( X ≥1) = P( x =1) + P(x =2)+P(x=3)
`P(X\geq 1) = 3_{C_(1) } (0.57)^(1) (0.43)^(3-1) + 3_{C_(2) } (0.57)^(2) (0.43)^(3-2) + 3_{C_(3) } (0.57)^(3) (0.43)^(3-3)`

`P(X\geq 1) = 3 (0.57) (0.43)^(2) + 3 (0.57)^(2) (0.43) + 1 (0.57)^(3) (0.43)^(0)`

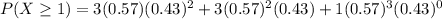
= 0.316179 + 0.419121 +0.185193

= 0.920493

Final answer:-

The probability that AT LEAST ONE of them has been vaccinated

P( X ≥1) = 0.920493

Answer 2

Answer:0.92

Explanation:

Given

`57\%` of Population is vaccinated

So, Probability of a person being vaccinated is
`P=0.57`

and simultaneously , probability of not vaccinated is
`1-P`

`=1-0.57=0.43`

Now, Probability that atleast one of them has been vaccinated is given by

`=1-P(\text{None of them is vaccinated})`

`=1-0.43* 0.43* 0.43`

`=1-0.0795`

`=0.92`