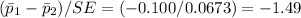Question

The housing commission of King County is interested in finding out more about the number of rental units that qualify as low-income housing but do not meet the minimum standard living requirements in Seattle and Renton. Units are randomly selected in both cities. Of the 85 low-income units sampled in Seattle (City 1), 17 do not meet minimum requirements. Of the 80 units sampled in Renton (City 2), 24 do not meet minimum requirements. The value of the z-statistic for testing equality of the proportion of low-income rental units that do not meet minimum standards in the two cities is

a) z=-2.33
b) none of these choices
c) Z=-1.96
d) Z= -1.49
e) z=-1.65

Answer 1

d) Z= -1.49

Explanation:

sample #1 ----->

first sample size,
`n_1= 85`

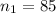
number of successes, sample 1 =
`x_1= 17`

proportion success of sample 1 ,

`\bar p_1= (x_1)/(n_1) = 0.2000000`

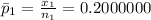
sample #2 ----->

second sample size,

`n_2 = 80`

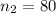
number of successes, sample 2 =
`x_2 = 24`

proportion success of sample 1 ,

`\bar p_2= (x_2)/(n_2) = 0.300000`

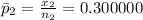
difference in sample proportions,

`\bar p_1 - \bar p_2 = 0.2000 - 0.3000 \\\\= -0.1000`

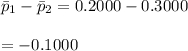
pooled proportion ,

`p = ( (x_1+x_2))/((n_1+n_2))\\\\= 0.2484848`

std error ,

`SE=\sqrt{p*(1-p)*((1)/(n_1)+(1)/(n_2) )} \\\\=0.06731`

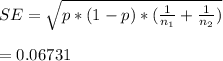
Z-statistic =
`(\bar p_1 - \bar p_2)/SE = ( -0.100 / 0.0673 ) = -1.49`