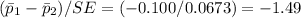Answer:
d) Z= -1.49
Explanation:
sample #1 ----->
first sample size,
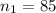
number of successes, sample 1 =
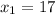
proportion success of sample 1 ,
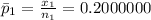
sample #2 ----->
second sample size,
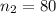
number of successes, sample 2 =
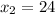
proportion success of sample 1 ,
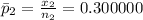
difference in sample proportions,
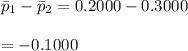
pooled proportion ,
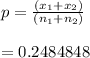
std error ,
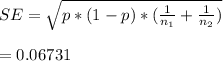
Z-statistic =