Answer:
Ejercicio 1
Las funciones exponenciales son;
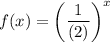
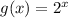
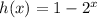
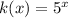
La función que no es exponencial se da de la siguiente manera;
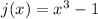
Exercise 2
a)
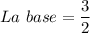
La función está aumentando ya que la base> 1
b) La base = (1,1)
La función aumenta a medida que la base> 1 es igual a 1
c)
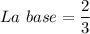
La función está disminuyendo ya que la base <1
d) La base = 0,75
La función está disminuyendo ya que la base <1
e) La base = 3
La función aumenta a medida que la base> 1
f) La base = e
La función aumenta a medida que la base> 1
Explanation:
Una función exponencial es una función en la que la variable independiente está presente en el exponente de la función
Las funciones se expresan de la siguiente manera;
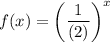
La función tiene la variable independiente en el exponente, por lo tanto, es una función exponencial
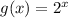
Del mismo modo, la función anterior tiene la variable independiente en el exponente, por lo tanto, es una función exponencial
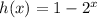
La función anterior tiene la variable independiente en el exponente, por lo tanto, es una función exponencial
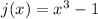
En la función anterior, la variable independiente no está en el exponente, por lo tanto, no es una función exponencial
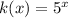
La función anterior tiene la variable independiente en el exponente, por lo tanto, es una función exponencial.
Exercise 2
a)
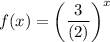
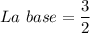
La función está aumentando ya que la base> 1
b) g(x) = (1,1)ˣ
The base = (1,1)
La función aumenta a medida que la base> 1
c)
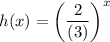
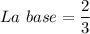
La función está disminuyendo ya que la base <1
d) k (x) = (0,75) ˣ
La base = 0,75
La función está disminuyendo ya que la base <1
e) m (x) = 3ˣ
La base = 3
La función aumenta a medida que la base> 1
f) n (x) = eˣ
La base = e
La función aumenta a medida que la base> 1