Question

A 350-km-long high-voltage transmission line 2.00 cm in diameter carries a steady current of 1,010 A. If the conductor is copper with a free charge density of 8.50 1028 electrons per cubic meter, how many years does it take one electron to travel the full length of the cable? (Use 3.156 107 for the number of seconds in a year.)

Answer 1

t = 47 years

Step-by-step explanation:

To find the number of years in which the electrons cross the complete transmission, you first calculate the drift velocity of the electrons in the transmission line, by using the following formula:

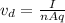`v_d=(I)/(nAq)` (1)

I: current = 1,010A

A: cross sectional area of the transmission line = π(d/2)^2

d: diameter of the transmission line = 2.00cm = 0.02 m

n: free charge density = 8.50*10^28 electrons/m^3

q: electron's charge = 1.6*10^-19 C

You replace the values of all parameters in the equation (1):

`v_d=(1010A)/((8.50*10^(28)m^(-3))(\pi(0.02m/2)^2)(1.6*10^(-19)C))\\\\v_d=2.36*10^(-4)(m)/(s)`

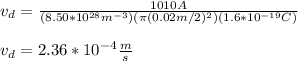
with this value of the drift velocity you can calculate the time that electrons take in crossing the complete transmission line:

`t=(d)/(v_d)=(350km)/(2.36*10^(-4)m/s)=(350000m)/(2.36*10^(-4)m/s)\\\\t=1,483,050,847\ s`

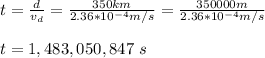
Finally, you convert this value of the time to years:

`t=1,483,050,847s*(1\ year)/(3.154*10^7s)=47\ years`

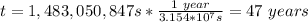
hence, the electrons take around 47 years to cross the complete transmission line.