Answer:
0.8 kilograms of fuel are consumed each second.
Step-by-step explanation:
As turbines are steady-state devices, the thermal efficiency of a turbine is equal to the percentage of the ratio of the output power to fluid power, that is:
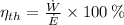
The fluid power is:
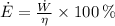
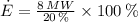
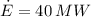
Which means that gas turbine consumes 40 megajoules of fluid energy each second, which is heated and pressurized with help of the fuel, whose amount of consumption per second is:
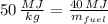
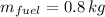
0.8 kilograms of fuel are consumed each second.