Question

A Broadway theater has 800 ​seats, divided into​ orchestra, main, and balcony seating. Orchestra seats sell for $ 40 comma main seats for $ 30 comma and balcony seats for $ 20.  If all the seats are​ sold, the gross revenue to the theater is $ 23 comma 200.  If all the main and balcony seats are​ sold, but only half the orchestra seats are​ sold, the gross revenue is $ 20 comma 000. How many are there of each kind of​ seat?

orchestra seats: main seats: balcony seats:

Answer 1

orchestra seats: main seats: balcony seats: 160: 400: 240

Explanation:

Let number of orchestra seats = x

Let number of main seats = y

Let number of balcony seats = z

As per given statement, total seats are 800

`x +y+z=800 ..... (1)`

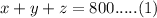
Sales price of each orchestra seat = $40

Sales price of each main seat = $30

Sales price of each balcony seat = $20

If all the seats are sold, total revenue is $23200.

`\Rightarrow 40x + 30y+20z=23200 ...... (2)`

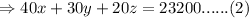
If all the main and balcony seats are​ sold, but only half the orchestra seats are​ sold, the gross revenue is $ 20 comma 000.

`\Rightarrow 40* (x)/(2) + 30y+20z=20000\\\Rightarrow 20x + 30y+20z=20000 ...... (3)`

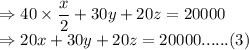
Here, we have 3 variables and 3 equations. Let us solve them.

Subtracting Equation (3) from equation (2):

`\Rightarrow 20x = 3200\\\Rightarrow x = 160`

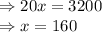
Putting value of x in equations (1) and (2):

Equation (1)

`\Rightarrow 160 +y+z=800\\\Rightarrow y+z=640 ...... (4)`

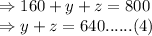
Equation (2)

`\Rightarrow 40* 160 +30y+20z=23200\\\Rightarrow 30y+20z=16800\\\Rightarrow 3y +2z=1680 ...... (5)`

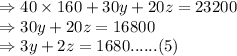
Equation (5) - 2
`*` Equation(4):

`\Rightarrow y =400`

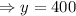
Putting value of y in equation (4):

`400 +z = 640\\\Rightarrow z =240`

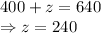
Hence, answer is:

orchestra seats: main seats: balcony seats: 160: 400: 240