Answer:
We conclude that there is an equal or larger proportion of Republicans in favor of lowering the standards.
Explanation:
The complete question is: A nationwide sample of influential Republicans and Democrats was asked as a part of a comprehensive survey whether they favored lowering environmental standards so that high-sulfur coal could be burned in coal-fired power plants. The results were:
Number sampled: 1,000 (republican) , 800 (democrats)
Number in favor: 200 (republican) , 168 (democrats)
At the 0.02 level of significance, can we conclude that there is a larger proportion of Democrats in favor of lowering the standards? Determine the p-value.
Let
 = proportion of Republicans in favor of lowering the standards.
= proportion of Republicans in favor of lowering the standards.
 = proportion of Democrats in favor of lowering the standards.
= proportion of Democrats in favor of lowering the standards.
SO, Null Hypothesis,
 :
:
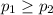 {means that there is an equal or larger proportion of Republicans in favor of lowering the standards}
{means that there is an equal or larger proportion of Republicans in favor of lowering the standards}
Alternate Hypothesis,
 :
:
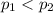 {means that there is a larger proportion of Democrats in favor of lowering the standards}
{means that there is a larger proportion of Democrats in favor of lowering the standards}
The test statistics that would be used here Two-sample z-test for proportions;
T.S. =
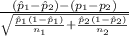 ~ N(0,1)
~ N(0,1)
where,
 = sample proportion of Republicans in favor of lowering the standards =
= sample proportion of Republicans in favor of lowering the standards =
 = 0.20
= 0.20
 = sample proportion of Democrats in favor of lowering the standards =
= sample proportion of Democrats in favor of lowering the standards =
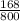 = 0.21
= 0.21
 = sample of Republicans = 1000
= sample of Republicans = 1000
 = sample of Democrats = 800
= sample of Democrats = 800
So, the test statistics =
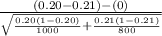
= -0.52
The value of z test statistics is -0.52.
Now, P-value of the test statistics is given by the following formula;
P-value = P(Z < -0.52) = 1 - P(Z
 0.52)
0.52)
= 1 - 0.6985 = 0.3015
Now, at 0.02 significance level, the z table gives a critical value of -2.054 for left-tailed test.
Since our test statistic is more than the critical value of z as -0.52 > -2.054, so we have insufficient evidence to reject our null hypothesis as it will not fall in the rejection region due to which we fail to reject our null hypothesis.
Therefore, we conclude that there is an equal or larger proportion of Republicans in favor of lowering the standards.