Answer:
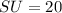
Explanation:
Given
Triangle TSU
Bisector TX
Required
Length of SU
A line is said to be a perpendicular bisector if and only if it divides a line segment into two equal lengths;
This means that line TX divides line SU into two equal part.
This implies that
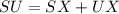
and
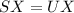
Substitute
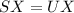 ; The expression becomes
; The expression becomes
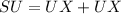
Recall that
 ;
;
So, the above expression becomes
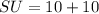
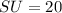
Hence, the length of is 20