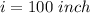Question

The city of Ventura would like to build a seawall to protect the city from the threat of tsunamis. Each additional inches of height further protects the city and the 100 residents are each willing to pay $10 per inch of seawall height, regardless of how many inches are provided. The cost of building a wall that is i inches high is given by c(i) = 6i^2. What is the Pareto Optimal height for the seawall?

Answer 1

The Pareto Optimal height is
`i = 100 \ inch`

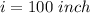
Explanation:

The Pareto Optimal height is a height of the seawall at which an increase in wall height will exceed the amount the resident are willing to pay and a decrease will affect the protection of the city

The number of residents is
`n = 100`

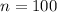
The amount each are willing to pay is
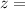`z=`$10 per inch

The cost of building a wall that is i inches high is given by
`c(i) = 6i^2.`

The total amount the residents are willing to pay is

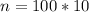`n = 100 * 10` = $1000

The maximum cost is mathematically represented as

`(dc(i))/(di) = 10i`

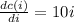
which implies that

1000 = 10i

Hence the Pareto Optimal height is

=>
`i = (1000)/(10)`

`i = 100 \ inch`